Difference between revisions of "BIP 0032"
| Line 90: | Line 90: | ||
Note that the fingerprint of the parent only serves as a checksum here, and software must be willing to deal with collisions. Internally, the full 160-bit identifier could be used. | Note that the fingerprint of the parent only serves as a checksum here, and software must be willing to deal with collisions. Internally, the full 160-bit identifier could be used. | ||
| + | |||
| + | When importing a serialized extended public key, implementations must verify whether the X coordinate in the public key data corresponds to a point on the curve. If not, the extended public key is invalid. | ||
===Master key generation=== | ===Master key generation=== | ||
| Line 142: | Line 144: | ||
==Security== | ==Security== | ||
| + | |||
| + | In addition to the expectations from the EC public-key cryptography itself: | ||
| + | * Given a public key K, an attacker cannot find the corresponding private key more efficiently than by solving the EC discrete logarithm problem (assumed to require 2<sup>128</sup> group operations). | ||
| + | , the intended security properties of this standard are: | ||
| + | * Given a child extended private key (k<sub>n</sub>,c<sub>n</sub>) and the integer n, an attacker cannot find the parent private key k<sub>par</sub> more efficiently than a 2<sup>256</sup> brute force of HMAC-SHA512. | ||
Private and public keys must be kept safe as usual. Leaking a private key means access to coins - leaking a public key can mean loss of privacy. | Private and public keys must be kept safe as usual. Leaking a private key means access to coins - leaking a public key can mean loss of privacy. | ||
Revision as of 14:29, 15 March 2013
|
This page describes a BIP (Bitcoin Improvement Proposal). |
BIP: 32 Title: Hierarchical Deterministic Wallets Author: Pieter Wuille Status: Draft Type: Informational Created: 11-02-2012
Contents
Abstract
This document describes hierarchical determinstic wallets (or "HD Wallets"): wallets which can be shared partially or entirely with different systems, each with or without the ability to spend coins.
The specification is intended to set a standard for deterministic wallets that can be interchanged between different clients. Although the wallets described here have many features, not all are required by supporting clients.
The specification consists of two parts. In a first part, a system for deriving a tree of keypairs from a single seed is presented. The second part demonstrates how to build a wallet structure on top of such a tree.
Motivation
The Bitcoin reference client uses randomly generated keys. In order to avoid the necessity for a backup after every transaction, (by default) 100 keys are cached in a pool of reserve keys. Still, these wallets are not intended to be shared and used on several systems simultaneously. They support hiding their private keys by using the wallet encrypt feature and not sharing the password, but such "neutered" wallets lose the power to generate public keys as well.
Deterministic wallets do not require such frequent backups, and elliptic curve mathematics permit schemes where one can calculate the public keys without revealing the private keys. This permits for example a webshop business to let its webserver generate a fresh addresses (public key hashes) for each order or for each customer, without giving the webserver access to the corresponding private keys (which are required for spending the received funds).
However, deterministic wallets typically consist of a single "chain" of keypairs. The fact that there is only one chain means that sharing a wallet happens on an all-or-nothing basis. However, in some cases one only wants some (public) keys to be shared and recoverable. In the example of a webshop, the webserver does not need access to all public keys of the merchant's wallet; only to those addresses which are used to receive customer's payments, and not for example the change addresses that are generated when the merchant spends money. Hierarchical deterministic wallets allow such selective sharing by supporting multiple keypair chains, derived from a single root.
Specification: Key derivation
Conventions
In the rest of this text we will assume the public key cryptography used in Bitcoin, namely elliptic curve cryptography using the field and curve parameters defined by secp256k1 (http://www.secg.org/index.php?action=secg,docs_secg). Variables below are either:
- integers modulo the order of the curve, serialized as 32 bytes, most significant byte first.
- coordinates of points on the curve, serialized as specified in SEC1 in compressed form: [0x02 or 0x03] + 32 byte x coordinate), where the header byte depends on the parity of the omitted y coordinate.
- byte sequences
Addition (+) of two coordinates is defined as application of the EC group operation. Multiplication (*) of an integer and a coordinate is defined as repeated application of the EC group operation. The generator element of the curve is called G. The public key K corresponding to the private key k is calculated as k*G. We do not distinguish between numbers or coordinates and their serialization as byte sequences.
Extended keys
In what follows, we will define a function that derives a number of child keys from a parent key. In order to prevent these from depending solely on the key itself, we extend both private and public keys first with an extra 256 bits of entropy. This extension, called the chain code, is identical for corresponding private and public keys, and consists of 32 bytes.
We represent an extended private key as (k,c), with k the normal private key, and c the chain code. An extended public key is represented as (K,c), with K the normal public key and c the chain code.
Child key derivation function
We define the child key derivation function CKD((kpar,cpar),n), which takes a parent extended secret key (kpar,cpar) and a 32-bit integer n, to produce a child extended secret key (kn,cn).
To define (kn,cn) = CKD((kpar,cpar),n):
- call I = HMAC-SHA512(Key=cpar, Data=kpar*G || n), where kpar*G is the public key corresponding to kpar, || is concatenation, and n is encoded as a 32 bits unsigned integer, most significant byte first.
- Split I into two 32-byte sequences, IL and IR.
- kn is equal to IL*kpar (mod n).
- cn is equal to IR.
In case IL is 0, the resulting key is invalid.
We also define a version that operates on extended public keys instead of private ones: (Kn,cn) = CKD'((Kpar,cpar),n):
- call I = HMAC-SHA512(Key=cpar, Data=Kpar || n), where n is encoded a 32 bits unsigned integer, most significant byte first.
- Split I into two 32-byte sequences, IL and IR.
- Kn is equal to IL*Kpar.
- cn is equal to IR.
In case IL is 0, the resulting key is invalid.
Note that the extended public key corresponding to the evaluation of CKD(x,n) is identical to the evaluation of CKD'(X,n), with X the extended public key corresponding to x. Symbolically, CKD(x,n)*G = CKD'(x*G,n). This implies that CKD' can be used to derive all public keys corresponding to the private keys that CKD would find. It cannot be used to retrieve the private keys, however.
The HMAC-SHA512 function is specified in RFC 4231.
The key tree
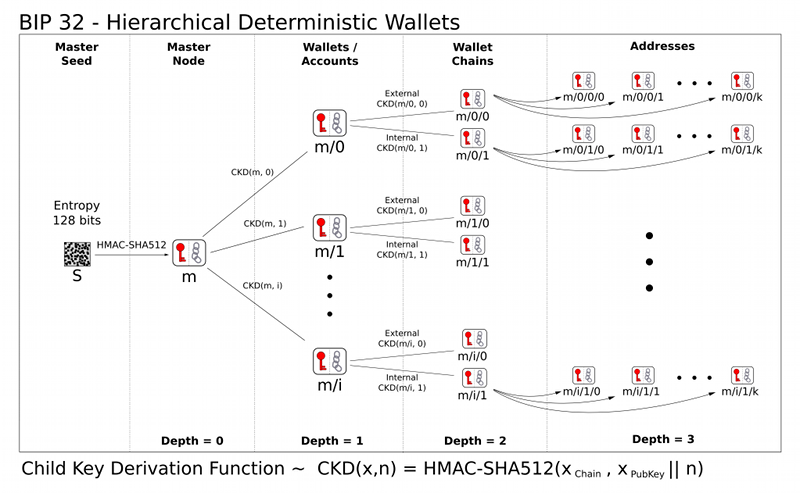
The next step is cascading several CKD constructions to build a tree. We start with one root, the master extended key m. By evaluating CKD(m,n) for several values of n, we get a number of first-degree derivative nodes. As each of these is again an extended key, CKD can be applied to those as well. To shorten notation, we will write CKD(CKD(CKD(m,n1),n2),n3) as m/n1/n2/n3 now.
Each leaf node in the tree corresponds to an actual keypair, while the internal nodes correspond to the collection of keypairs that descends from them. The chain codes of the leaf nodes are ignored, and only their embedded private or public key is used. Because of this construction, knowing an extended private key allows reconstruction of all descendant private keys and public keys, and knowing an extended public keys allows reconstruction of all descendant public keys.
Key identifiers
Extended keys can be identified by the Hash160 (RIPEMD160 after SHA256) of the serialized public key, ignoring the chain code. This corresponds exactly to the data used in traditional Bitcoin addresses. It is not advised to represent this data in base58 format though, as it may be interpreted as an address that way (and wallet software is not required to accept payment to the chain key itself).
The first 32 bits of the identifier are called the fingerprint.
Serialization format
Extended public and private keys are serialized as follows:
- 4 byte: version bytes (mainnet: 0x0488B21E public, 0x0488ADE4 private; testnet: 0x043587CF public, 0x04358394 private)
- 1 byte: depth: 0x00 for master nodes, 0x01 for level-1 descendants, ....
- 4 bytes: the fingerprint of the parent's key (0x00000000 if master key)
- 4 bytes: child number. This is the number n in xn = xpar/n, with xn the key being serialized. This is encoded in MSB order. (0x00000000 if master key)
- 32 bytes: the chain code
- 33 bytes: the public key or private key data (0x02 + X or 0x03 + X for public keys, 0x00 + k for private keys)
This 78 byte structure can be encoded like other Bitcoin data in Base58, by first adding 32 checksum bits (derived from the double SHA-256 checksum), and then converting to the Base58 representation. This results in a Base58-encoded string of up to 112 characters. Because of the choice of the version bytes, the Base58 representation will start with "xprv" or "xpub" on mainnet, "tprv" or "tpub" on testnet.
Note that the fingerprint of the parent only serves as a checksum here, and software must be willing to deal with collisions. Internally, the full 160-bit identifier could be used.
When importing a serialized extended public key, implementations must verify whether the X coordinate in the public key data corresponds to a point on the curve. If not, the extended public key is invalid.
Master key generation
The total number of possible extended keypairs is almost 2^512, but the produced keys are only 256 bits long, and offer about half of that in terms of security. Therefore, master keys are not generated directly, but instead from a potentially short seed value.
- Generate a seed S of a chosen length (at least, but not limited to, 128 bits) from a (P)RNG.
- Calculate I = HMAC-SHA512(key="Bitcoin seed", msg=S)
- Split I into two 32-byte sequences, IL and IR.
- Use IL (mod n) as master secret key, and IR as master chain code.
In case IL is 0, the master key is invalid.
Specification: Wallet structure
The previous sections specified key trees and their nodes. The next step is imposing a wallet structure on this tree.
An HDW is organized as several 'accounts'. Accounts are numbered, the default account ("") being number 0. Clients are not required to support more than one account - if not, they only use the default account.
Each account is composed of two keypair chains: an internal and an external one. The external keychain is used to generate new public addresses, while the internal keychain is used for all other operations (change addresses, generation addresses, ..., anything that doesn't need to be communicated). Clients that do not support separate keychains for these should use the external one for everything.
* m/i/0/k corresponds to the k'th keypair of the external chain of account number i of the HDW derived from master m. * m/i/1/k corresponds to the k'th keypair of the internal chain of account number i of the HDW derived from master m.
Use cases
Full wallet sharing: m
In cases where two systems need to access a single shared wallet, and both need to be able to perform spendings, one needs to share the master private extended key. Nodes can keep a pool of N look-ahead keys cached for external chains, to watch for incoming payments. The look-ahead for internal chains can be very small, as no gaps are to be expected here. An extra look-ahead could be active for the first unused account's chains - triggering the creation of a new account when used. Note that the name of the account will still need to be entered manually and cannot be synchronized via the block chain.
Audits: M
In case an auditor needs full access to the list of incoming and outgoing payments, one can share the master public extended key. This will allow the auditor to see all transactions from and to the wallet, in all accounts, but not a single secret key.
Per-office balances: m/i
When a business has several independent offices, they can all use wallets derived from a single master. This will allow the headquarters to maintain a super-wallet that sees all incoming and outgoing transactions of all offices, and even permit moving money between the offices.
Recurrent business-to-business transactions: M/i/0
In case two business partners often transfer money, one can use the extended public key for the external chain of a specific account (M/i/0) as a sort of "super address", allowing frequent transactions that cannot (easily) be associated, but without needing to request a new address for each payment. Such a mechanism could also be used by mining pool operators as variable payout address.
Unsecure money receiver: M/i/0
When an unsecure webserver is used to run an e-commerce site, it needs to know public addresses that be used to receive payments. The webserver only needs to know the public extended key of the external chain of a single account. This means someone illegally obtaining access to the webserver can at most see all incoming payments, but will not (trivially) be able to distinguish outgoing transactions, nor see payments received by other webservers if there are several ones.
Compatibility
To comply with this standard, a client must at least be able to import an extended public or private key, to give access to its direct descendants as wallet keys. The wallet structure (master/account/chain/subchain) presented in the second part of the specification is advisory only, but is suggested as a minimal structure for easy compatibility - even when no separate accounts or distinction between internal and external chains is made. However, implementations may deviate from it for specific needs; more complex applications may call for a more complex tree structure.
Security
In addition to the expectations from the EC public-key cryptography itself:
- Given a public key K, an attacker cannot find the corresponding private key more efficiently than by solving the EC discrete logarithm problem (assumed to require 2128 group operations).
, the intended security properties of this standard are:
- Given a child extended private key (kn,cn) and the integer n, an attacker cannot find the parent private key kpar more efficiently than a 2256 brute force of HMAC-SHA512.
Private and public keys must be kept safe as usual. Leaking a private key means access to coins - leaking a public key can mean loss of privacy.
Somewhat more care must be taken regarding extended keys, as these correspond to an entire (sub)tree of keys. One weakness that may not be immediately obvious, is that knowledge of the extended public key + a private key descending from it is equivalent to knowing the extended private key (i.e., every private and public key). This means that extended public keys must be treated more carefully than regular public keys.
We rely on resistance against (partial) preimages in HMAC-SHA512 to prevent IL in key derivation and master key generation from being zero.
Test Vectors
Come back soon!
Acknowledgements
- Gregory Maxwell for the original idea of type-2 deterministic wallets, and many discussions about it.
- Alan Reiner for the implementation of this scheme in Armory, and the suggestions that followed from that.
- Mike Caldwell for the version bytes to obtain human-recognizable Base58 strings.